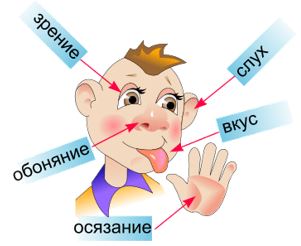
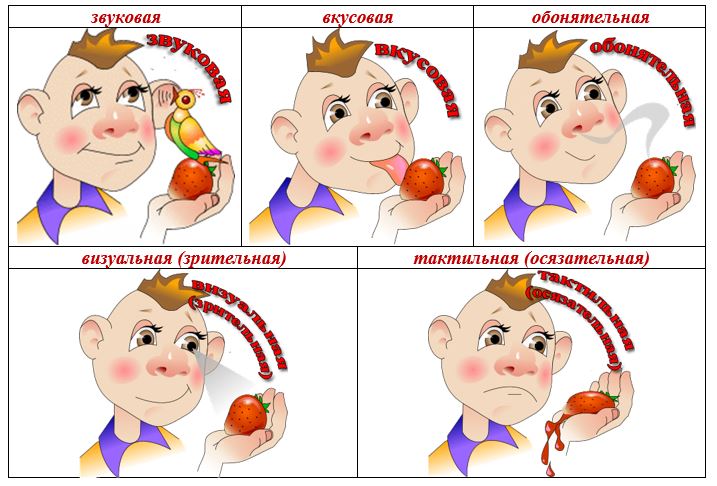
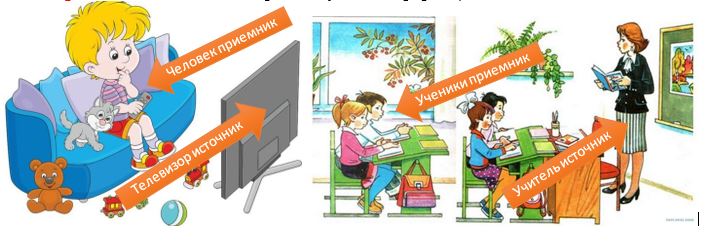
Цель урока: изучить представление информации в компьютере. её кодирование и единицы измерения объёма.
Краткий конспект
Код – совокупность условных знаков, каждому из которых присваивается определенное значение
Двоичный код – набор из нулей и единиц.
Кодирование – преобразование входной информации в форму, воспринимаемую компьютером.
Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
Бит – одна двоичная цифра: 0 или 1.
Байт – единица измерения количества информации, состоящая из восьми последовательных и взаимосвязанных битов.
Байт – это объём информации, который отводится для хранения цифрового кода одного символа
1 байт= 8 бит
Например: фраза “Средняя школа” занимает в памяти 13 байт=104 бит.
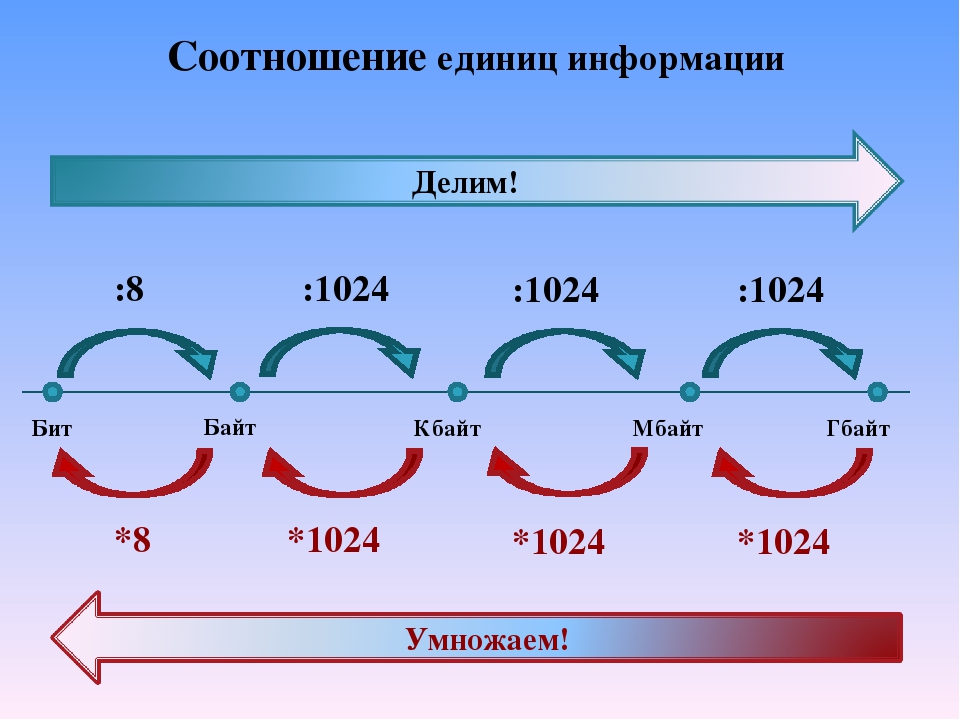
Для обозначения большего объема информации используются другие единицы измерения:
1 Кбайт (килобайт) = 1 024 байт;
1 Мбайт (мегабайт) = 1 024 Кбайт = 1 048 576 байт;
1 Гбайт (гигабайт) = 1 024 Мбайт = 1 048 576 Кбайт = 1 073 741 824 байт;
1 Тбайт (терабайт) = 1 024 Гбайт = 1 048 576 Мбайт = 1 073 741 824 Кбайт = 1 099 511 627 776 байт.
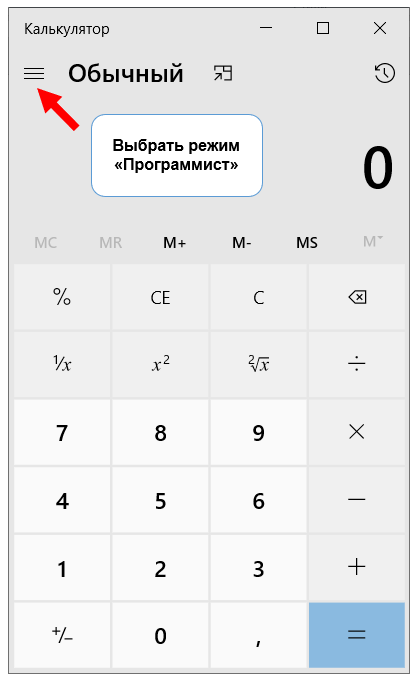
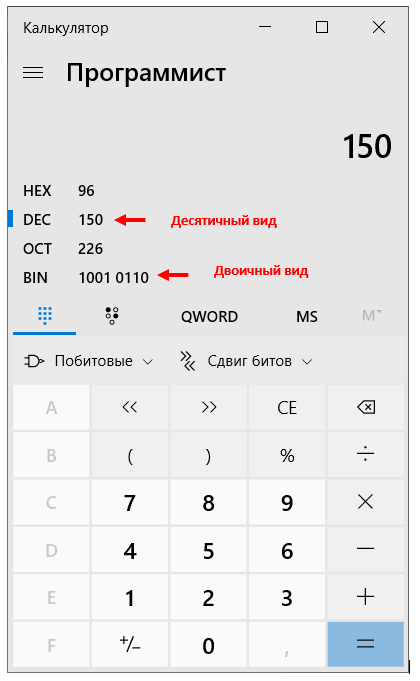
Для перевода чисел можно воспользоваться программой Калькулятор.
Для этого откройте программу Калькулятор. В панели навигации выбрать Вид —> Программист.

Задания по теме урока
Задание 1. Выполните тест по ссылке
Задание 2. Найдите пары
Дополнительные задания:

Домашнее задание
§ 2 учебного пособия, ответить на вопросы после параграфа.